Home > NEWS > Introduction to Spherical Lens
Spherical lens refers to a type of optical lens with one or two surface shaped like a cut of sphere, meaning this surface can be defined from a center reference point and a fix radius of curvature. Spherical lens are the more commons form of optical lens, being easier to design, easier to manufacture and easier to check the quality. In this article, we'll introduce you to the world of spherical lenses, discussing discussing about spherical lenses.
A spherical lens is a portion of a sphere that acts as a reflective surface. This surface can be either convex or concave. A concave spherical lens has an inwardly curved reflecting surface that reflects light inward, while a convex spherical lens has a raised reflective surface that reflects light outward. The substrate materials used to make spherical lenses include optical glass, ultraviolet fused quartz, infrared fused quartz, calcium fluoride (CaF2), magnesium fluoride (MgF2), zinc selenide (ZnSe), germanium (Ge), silicon (Si), and others. These materials can be coated with various optical films such as anti-reflective, highly reflective, beam splitting, and metal films. Wideband antireflective films are capable of reducing reflection in the ultraviolet, visible, near-infrared, and mid-infrared bands.
A lens is classified as thin when its center is so small that its optical characteristics are independent of its shape, whether it is a convex lens with a biconvex, planoconvex, or concave-convex shape, or a concave lens with a double concave, flat-concave, or convex-concave shape. In this case, the influence of the thickness at the center of the lens on its optical properties can be disregarded, and the lens can be referred to as a thin lens. A double-headed arrow pointing towards each other is used to represent a convex thin lens, while a double-headed arrow pointing away from each other represents a concave thin lens.
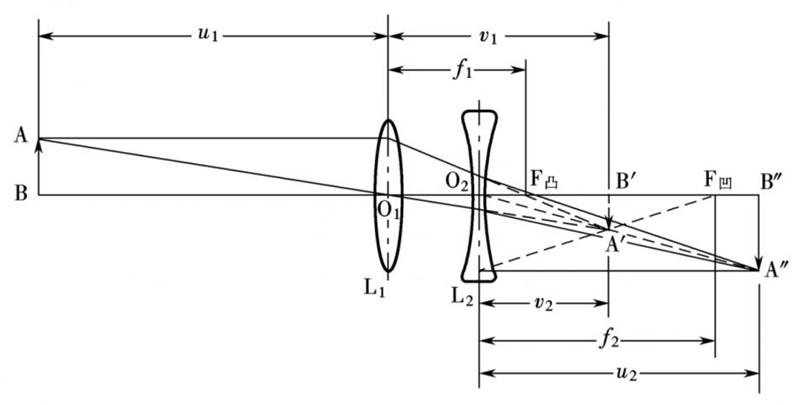
Concave mirror: A spherical mirror with the inner side of the spherical surface as a reflecting surface is called a concave mirror. Convex lenses can be divided into three forms: double convex, flat-convex, and concave-convex.
Convex mirror: A spherical mirror with the outside of the spherical surface as the reflecting surface is called a convex mirror. Concave lenses can be divided into three forms: double concave, flat-concave, and convex concave.
Spherical lenses are used for a wide range of applications, including but not limited to:
Photography and Videography
Spherical lenses are commonly used in cameras and videography equipment to focus light and produce clear and sharp images. They can also be used to create special effects, such as bokeh and depth of field.
Astronomy
Telescopes use spherical lenses to gather and focus light from distant objects in space. They are also used to correct for chromatic aberration, which is a distortion of colors that occurs when light passes through a lens.
Medicine
Spherical lenses are used in various medical devices, such as microscopes and endoscopes, to magnify and focus the light on the area of interest.
Manufacturing
Spherical lenses are used in the manufacturing industry to inspect and measure small parts and components.
A spherical lens is a lens with a curved surface that is part of a sphere. The focal length of a spherical lens is the distance between the lens and the point at which parallel rays of light converge (or appear to converge) after passing through the lens. The focal length of a spherical lens is dependent on the curvature of its surfaces and the refractive index of the material from which it is made.
The formula for calculating the focal length of a thin spherical lens (i.e., one with a negligible thickness compared to its radius of curvature) is:
1/f = (n - 1) * (1/R1 - 1/R2)
Where:
f is the focal length of the lens
n is the refractive index of the lens material
R1 is the radius of curvature of the first lens surface (measured from the center of the sphere)
R2 is the radius of curvature of the second lens surface (also measured from the center of the sphere)
If the lens has a symmetrical shape, i.e., R1 = R2, then the formula can be simplified to:
1/f = (n - 1) * (2/R)
Where R is the radius of curvature of either lens surface.
Note that this formula assumes that the incident light rays are parallel to the lens axis, which is the line passing through the centers of curvature of the lens surfaces. In practice, the lens may be used with light rays that are not parallel to the axis, in which case the focal length will vary depending on the angle of incidence.
IMPACT ON SPHERICAL LENS COST
| Factor | Impact on Cost |
|---|---|
| Material | Different materials have different costs, with more specialized or exotic materials often costing more |
| Size | Generally, larger lenses cost more than smaller ones due to the increased amount of material required to produce them. |
| Quality | Higher quality lenses may have more precise tolerances and better coatings, which can increase their cost. |
| Manufacturing Process | Different manufacturing processes can affect the cost of lenses, with more advanced or specialized processes often costing more. |
| Intended Use | Lenses designed for specialized applications, such as medical or scientific instruments, may cost more due to the precision and specialized features required. |
| Quantity | Bulk orders of lenses can often be produced at a lower cost per unit, so the quantity ordered can impact the overall cost. |
| Market Conditions | The cost of materials and other factors can fluctuate over time due to market conditions, which can impact the final cost of the lens. |
FAQs:
1. What is the difference between a spherical lens and an aspherical lens?
A spherical lens has a constant curvature across its surface, while an aspherical lens has a varying curvature that helps reduce spherical aberration and other distortions.
2. How do I clean my spherical lens?
Use a microfiber cloth and lens cleaning solution to gently wipe the lens surface, avoiding any scratches or damage.
3. Can I use a convex lens as a magnifying glass?
Yes, a convex lens can be used as a magnifying glass to magnify small objects.
4. What is the best spherical lens for portrait photography?
A prime lens with a wide aperture, such as a 50mm f/1.4 lens, is ideal for portrait photography.
5. Can a concave lens be used in a camera?
No, concave lenses are not suitable for cameras as they diverge light and produce a smaller image.
OPIE (OPTICS & PHOTONICS International Exhibition 2024)
Apr. 17, 2024Happy International Women's Day!
Mar. 08, 2024How to calculate laser energy and power
Feb. 28, 2024
Copyright © SiChuan JUKA Optical Technology All Rights Reserved | Sitemap
